Exercices

Les trois premiers exercices sont à chercher sur feuille.

Exercice 1

On donne la fonction mystere_1 sans paramètre.

def mystere_1():
    a = 2
    b = 5
    c = a + b
    return c

1. Que renvoie la fonction suite à son exécution?

2. Est-il possible de modifier les valeurs des variables a et b en dehors de la fonction? Justifier.

3. Comment modifier la fonction pour pouvoir modifier les valeurs des variables a et b et qu’elle renvoie leur somme ?

Exercice 2

On donne la fonction mystere_2 ayant pour paramètre le nombre x.

def mystere_2(x):
    y = x**2
    y = y - x
    return y

1. Que renvoie l’appel mystere_2(7) ? et mystere_2(-4) ?

2. On supprime l’instruction return y. Que renvoie la fonction ?

3. Est-il possible d’obtenir les mêmes valeurs sans utiliser la variable locale y ? Si oui, comment ?

Exercice 3

On donne la fonction mystere_3 ayant pour paramètres les nombres a, b et c.

def mystere_3(a,b,c):
    d = b**2
    d = d - 4*a*c
    print(d)

1. Combien d’arguments faut-il ajouter lors de l’appel de la fonction mystere_3 ? Donner un exemple d’appel.

2. Comment appelle-t-on la variable d de la fonction mystere_3 ?

3. On exécute l’appel : D = mystere_3(1,2,3). Quelle est la valeur de la variable D ?

Exercice 4

On considère la figure suivante:

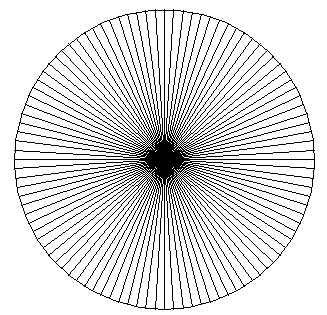
Cette figure réalisée avec le module turtle a été obtenue grâce au code suivant:

from turtle import *

def angle(n):
    return 180-360/n

def roue(r,n):
    circle(r)
    left(90)
    for i in range(n):
        forward(r)
        a = angle(n)
        right(a)
        forward(r)
        left(180)

1. Remplacer le calcul de la variable angle par la fonction angle qui prend en paramètre le nombre de rayons et qui renvoie la mesure de l’angle entre 2 rayons consécutifs.

2. Insérer dans la boucle for l’appel à la fonction angle pour obtenir l’angle de rotation de la tortue.

3. Créer la fonction roue qui a pour paramètres r et n et qui effectue le tracé de la roue de rayon r avec n rayons.

4. Écrire le code principal pour réaliser la roue de rayon 100 avec 20 rayons.

Exercice 5

Cet exercice nécessite l’import du module turtle pour effectuer les tracés.

1. La fonction carre prend en paramètre une longueur c et dessine un carré dont le côté mesure c.

   1. Écrire le code de la fonction carre.

   2. Réaliser un carré de côté 120.

2. La fonction triangle prend en paramètre une longueur t et dessine un triangle équilatéral dont le côté mesure t.

   1. Écrire le code de la fonction triangle.

   2. Réaliser un triangle de côté 120.

3. La fonction hexagone prend en paramètre une longueur h et dessine un hexagone régulier dont le côté mesure h.

   1. Écrire le code de la fonction hexagone.

   2. Réaliser un hexagone de côté 120.

4. Quel programme principal utilisant les trois fonctions précédentes permet d’obtenir la figure ci-dessous ?

   

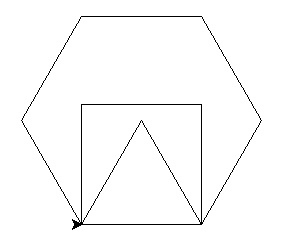
5. On peut remarquer que les trois fonctions carre, triangle et hexagone ont de nombreux points communs.

   1. Remplacer ces trois fonctions par une seule fonction nommée polygone qui a pour paramètres une longueur de côté et le nombre de côtés de la forme à dessiner.

   2. Écrire le programme principal pour obtenir la figure précédente.

   3. Remplacer le programme principal par une boucle afin de dessiner 8 formes régulières différentes.

   

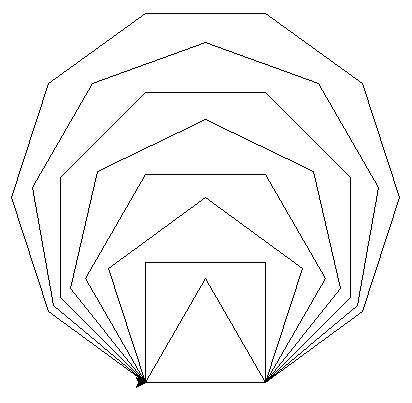
Exercice 6

On reprend le code de l’exrcice précédent.

Modifier ce code pour que chaque nouveau polygone construit ait pour côté un côté du polygone précédent comme le montre la figure suivante.

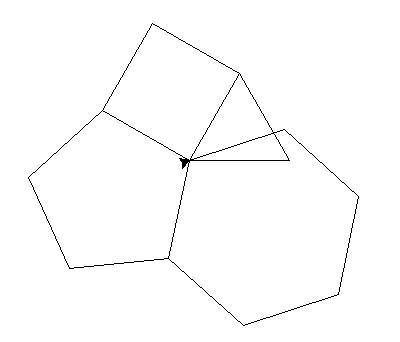
Exercice 7

1. Créer une fonction somme_carre qui prend en paramètre deux nombres a et b et renvoie la somme des carrés des deux nombres.

2. Créer une fonction double_produit qui prend en paramètre deux nombres a et b et renvoie le double du produit de ces deux nombres.

3. On veut créer une fonction id_rem qui prend en paramètre deux nombres a et b et renvoie le carré de la somme de ces deux nombres. Écrire cette fonction en utilisant les fonctions somme_carre et double_produit.

Exercice 8

1. Créer une fonction somme_arithm qui prend en paramètre un nombre entier N et renvoie la somme de tous les nombres entiers inférieurs ou égaux à N.

2. Créer une fonction somme_carre qui prend en paramètre un nombre entier N et renvoie la somme des carrés des nombres entiers inférieurs ou égaux à N.